En teoría de grafo, un árbol es un grafo en el que cualesquiera dos vértices están conectados por exactamente un camino.
Un bosque es una unión disjunta de árboles, un árbol a veces recibe el nombre de árbol libre.
Es decir, si se
cumple una de ellas otras también se cumplen. Para árboles finitos
además se cumple que: Si un árbol G tiene un número finito de vertices, n, entonces tiene n − 1 aristas.
- Un Grafo (o grafo no dirigido) es un conjunto V de vértices y un conjunto E de aristas tales que cada arista e ? E(queda asociada a un par no ordenado de vértices. Si existe una única arista e asociada con los vértices v y w, escribimos e = (v,w). En este contexto (v,w) denota una arista en un grafo no dirigido y no un par ordenado.
- Un grafo dirigido (o digrafo) consta de un conjunto finito de vértices V y un conjunto de arcos E ? V × V (obsérvese que cada arco es un par ordenado de vértices).
- Grafo conexo: un grafo G es conexo si dados cualesquiera dos vértices v y w en G, existe un camino de v a w.
- Camino: sean v0 y vn vértices de un grafo. Un camino de v0 a vn de longitud n es una sucesión alternante de n+1 vértices y n aristas que comienza con el vértice v0 y termina con el vértice vn.
- Longitud del camino: es el número de aristas que contiene.
- Ciclo: sean v y w vértices en un grafo G, un ciclo o circuito es un camino de longitud distinta de 0 de v a w, sin aristas repetidas.
- Subgrafo: sea G (V, E) un grafo. (V", E") es un subgrafo de G si
-
a) V" ( V y E"( E.
-
b) Para cada arista e" ( E", si e"
es incidente en v" y w", entonces v", w" ( V).
- Grafo con pesos (o poderado): es un grafo en el cual se le asignan valores a las aristas y la longitud del camino de un grafo con pesos es la suma de todos los pesos de las aristas en la ruta (camino).
Recorrido de un grafo
Recorrido en anchura:
El recorrido en anchura supone recorrer el grafo, a partir de un
nodo dado, en niveles, es decir, primero los que están a una distancia
de un arco del nodo de salida, después los que están a dos arcos de
distancia, y así sucesivamente hasta alcanzar todos los nodos a los que
se pudiese llegar desde el nodo salida.
Recorrido en profundidad:
el recorrido en profundidad trata de buscar los caminos que parten
desde el nodo de salida hasta que ya no es posible avanzar más. Cuando
ya no puede avanzarse más sobre el camino elegido, se vuelve atrás en
busca de caminos alternativos, que no se estudiaron previamente
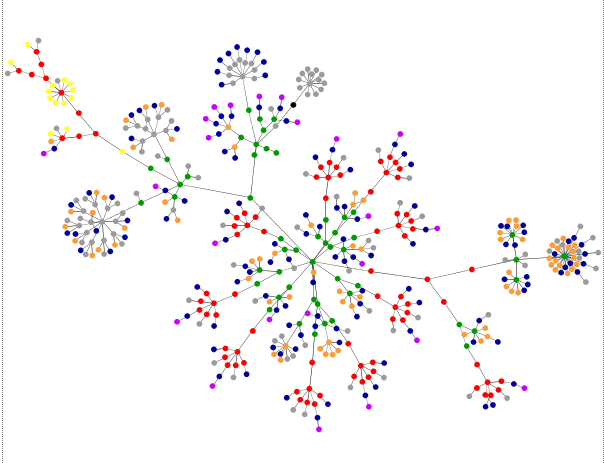
Un árbol es un grafo simple no dirigido G que satisface:
- G es conexo y no tiene ciclos .
- G no tiene ciclos y, si se añade alguna arista se forma un ciclo.
- G es conexo y si se le quita alguna arista deja de ser conexo.
- G es conexo y el grafo completo de 3 vértices
 no es un menor de G.
no es un menor de G. - Dos vértices cualquiera de G están conectados por un único camino simple.

No hay comentarios:
Publicar un comentario